Supervision: Konstantinos Pitas
Project type:
Semester project (master)
Master thesis
Finished
Project Description
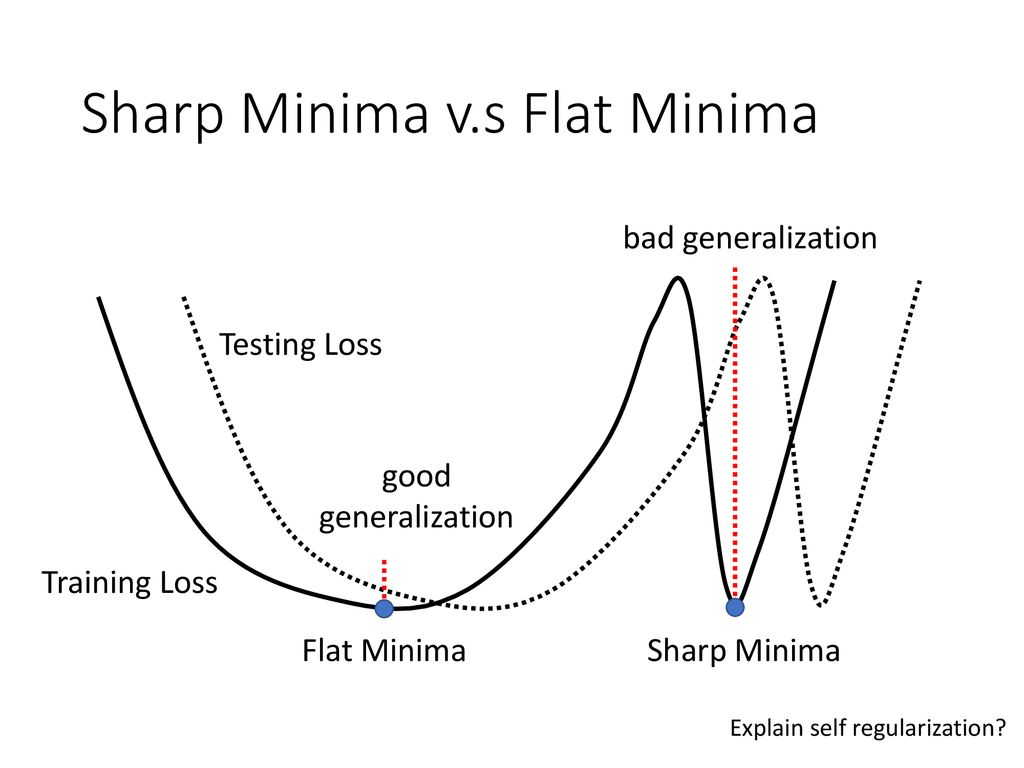
Predicting how a deep neural network will perform on new datapoints after training is important in real applications. One interesting quantity to check is how flat is the minimum after optimization.
Flat minima have links to good test accuracy in deep neural networks [1]. However such links are motivated by experiments that show simple empirical correlations between flatness and good test accuracy.
A main problem hindering more formal results is the significant computational complexity involved.
The Hessian matrix of the loss with respect to the deep neural network parameters, which captures curvature, has dimensions dxd with d being the number of parameters. Thus for deep neural networks this matrix is huge and various approximations are used to compute and store it [2][3].
Furthermore the curvature captured by the Hessian is a local property. However one would want it to hold for a wide area around the minimum. In the non-convex case of deep neural networks this is difficult to prove and even test empirically.
Project Goals
In this project the student will test empirically and explore ways to accurately characterize the quality of various approximations to the Hessian matrix for small and moderate deep learning problems.
Prerequisites
The student must be highly motivated and independent with good knowledge of Python, Tensorflow/Keras and/or Pytorch.
The project consists of 20% theory and 80% application and but has links to a number of interesting problems in deep neural network theory.
This is a master or semester project.
Contact Contact me by email at konstantinos.pitas@epfl.ch or pass by ELE 227 for a quick discussion.
[1] Keskar, Nitish Shirish, et al. "On large-batch training for deep learning: Generalization gap and sharp minima." arXiv preprint arXiv:1609.04836 (2016).
[2] Martens, James, and Roger Grosse. "Optimizing neural networks with kronecker-factored approximate curvature." International conference on machine learning. 2015.
[3] Mishkin, Aaron, et al. "Slang: Fast structured covariance approximations for bayesian deep learning with natural gradient." Advances in Neural Information Processing Systems. 2018.